11 Losgr¨oßenplanung bei Werkstattproduktion
11.1 Einf¨uhrung, ABC -A nalyse
Materialbedarf
• programmorientierte (Losgr¨oßen- und) Bedarfsplanung
• stochastische Bedarfsprognose
• Prim¨arbeda rf
• Sekund¨arbedarf
• Terti¨arbedarf
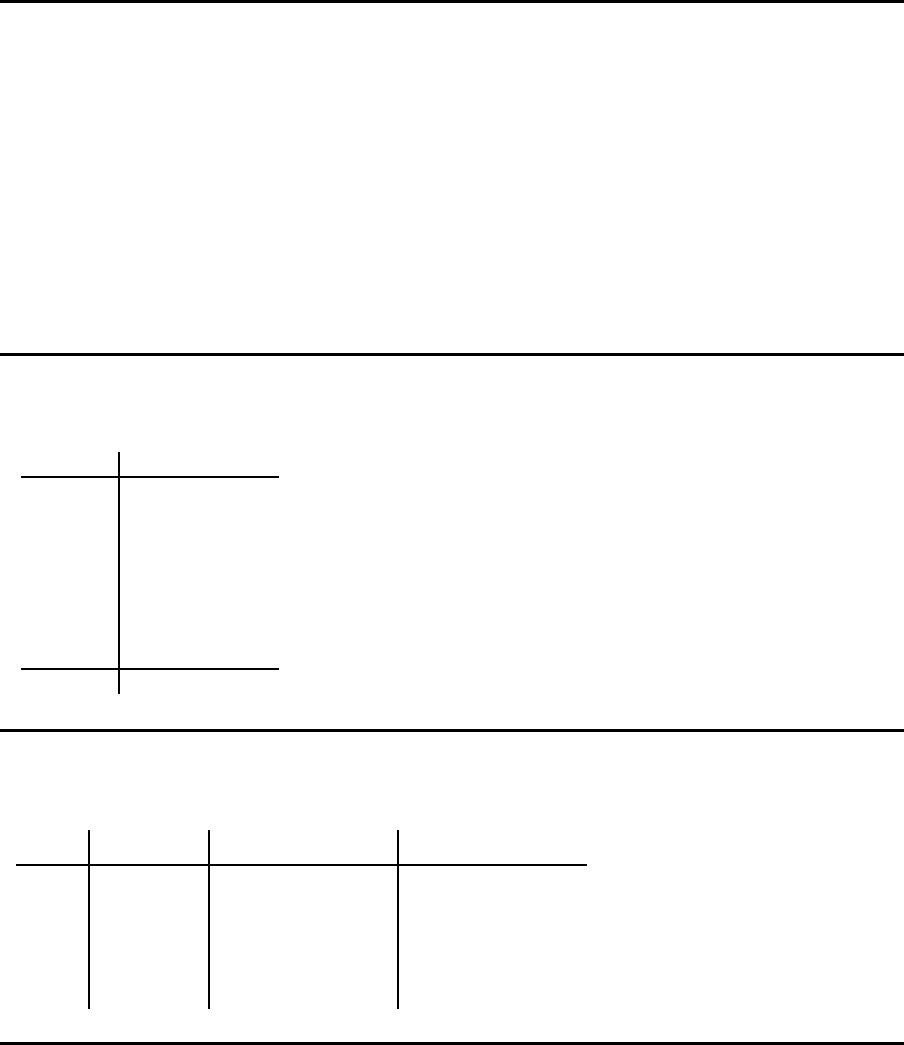
ABC-Analyse
Daten
Produkt
Verbrauchswert
1 1 0
2 130
3
5
4 780
5
20
6 3 0
7 450
8
25
Summe 1450
ABC-Analyse
Ergebnisse
Produkt
Verbrauchswert
kumulierter Anteil an der
Anzahl der Produkte (%)
kumulierter Anteil am
Verbrauchswert (%)
4 780 12.5 53.79
7 450 25.0 84.83
2 130 37.5 93.79
6
30 50.0 95.86
8 25 62.5 97.59
5 20 75.0 98.97
1
10 87.5 99.66
3 5 100.0 100.00
50
ABC-Analyse
0
10
20
30
40
50
60
70
80
90
100
(kumuliert, in %)
Verbrauchswert je Periode
0 10 20 30 40 50 60 70 80 90 100
Anzahl der Verbrauchsfaktorarten
(kumuliert, in %)
A B C
11.2 Programmorientierte Bedarfsermittlung
• Hauptproduktionsprogramm
• Erzeugnisz usammenhang
• Durchlaufzeiten, Wiederbeschaffungszeiten
• Lagerbest¨a nde
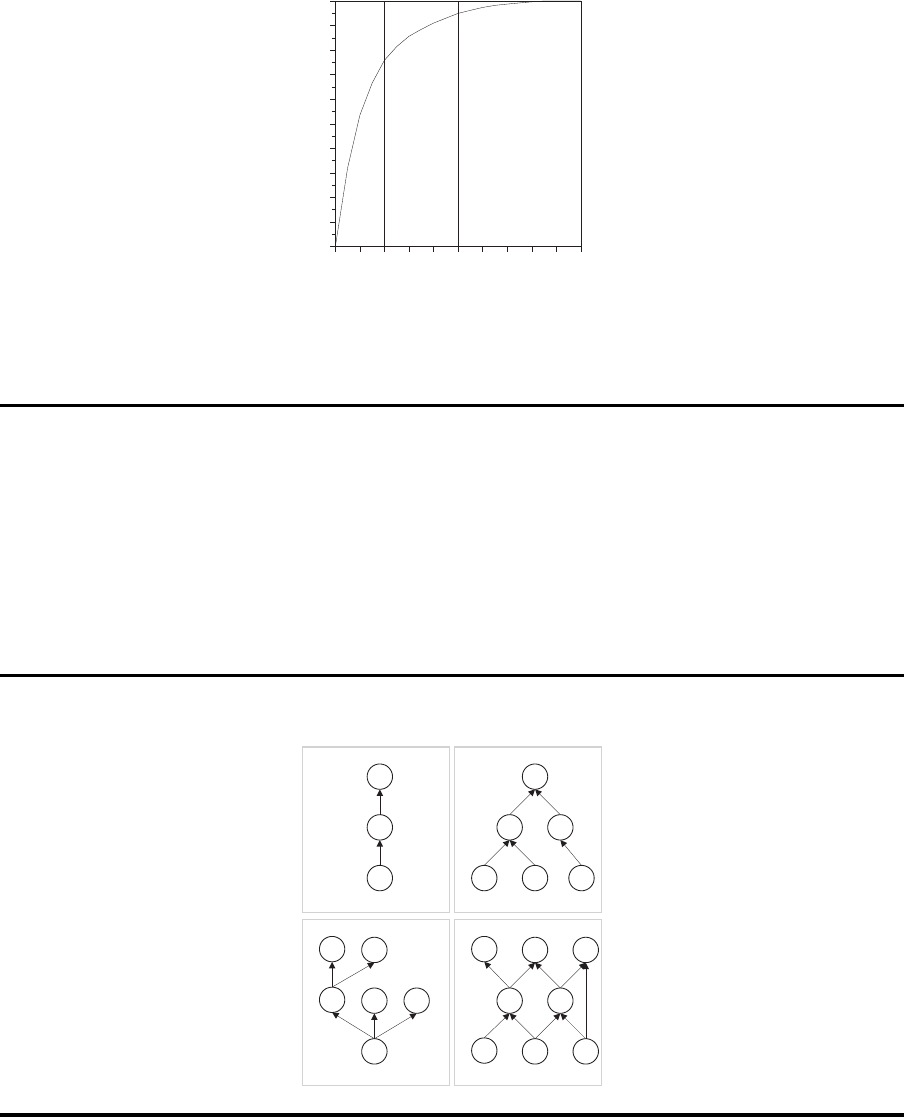
Darstellung d er Erzeugnisstruktur - Gozintograph
P1
B1
E1
P1
P2
P3 P4
B1
E1
P1
P2 P3
B1 B2
E1
E2 E3
P1
B1 B2
E1 E2 E3
b) konvergierenda) linear
c) divergierend d) generell
Darstellung d er Erzeugnisstruktur - Gozintograph - generell
51
1
1
1
1
1
1
1
1
1
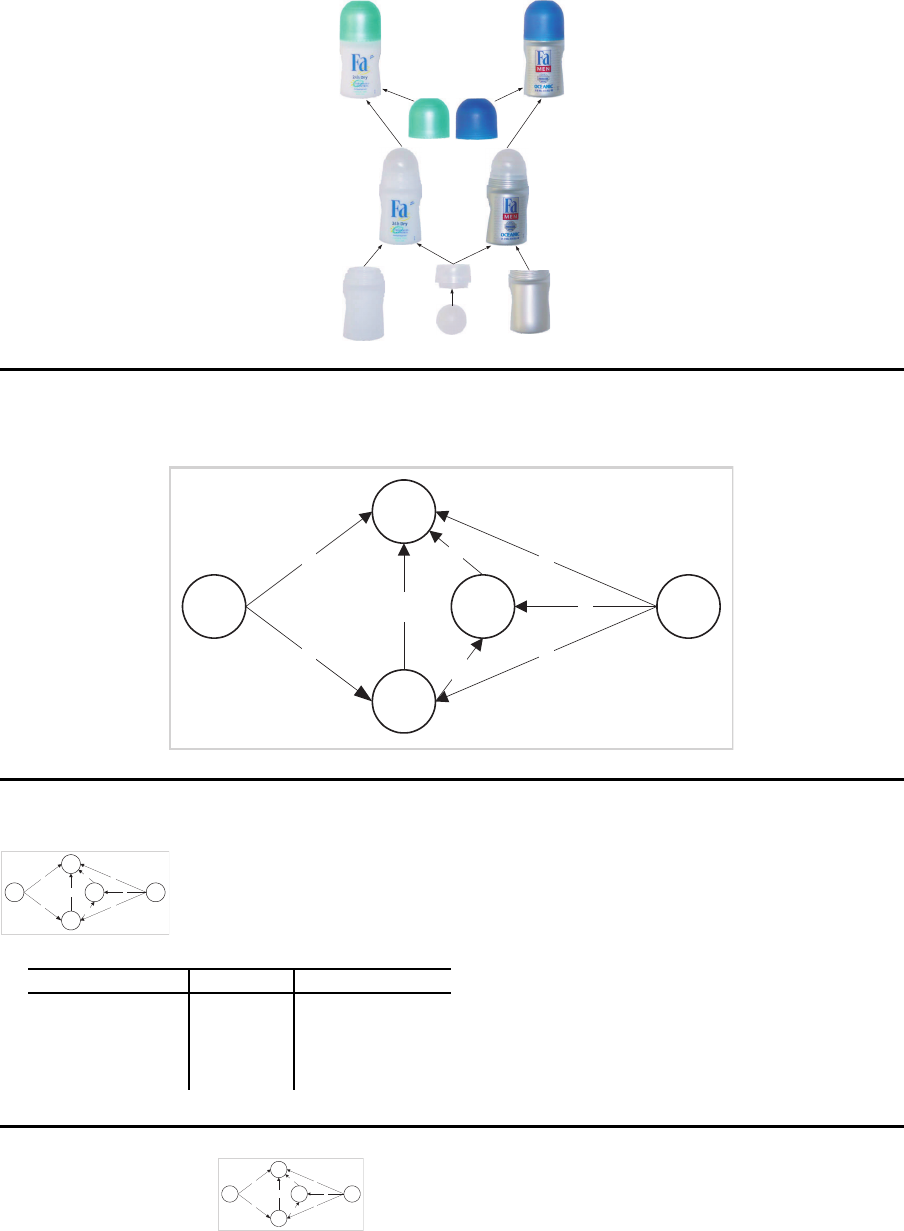
St¨ucklisten
Beispiel
P1
E1 B1
B2
E2
3
2
1
2
4
5 2
2
Mengen¨ubersichtsst¨uckliste
P1
E1 B1
B2
E2
3
2
1
2
4
5 2
2
Erzeugnis P1
Sachnummer Menge Bezeichnung
B1 2 Baugruppe
B2 5 Baugruppe
E1
28 Einzelteil
E2 20 Einzelteil
Baukastenst¨ucklisten
P1
E1 B1
B2
E2
3
2
1
2
4
5 2
2
52
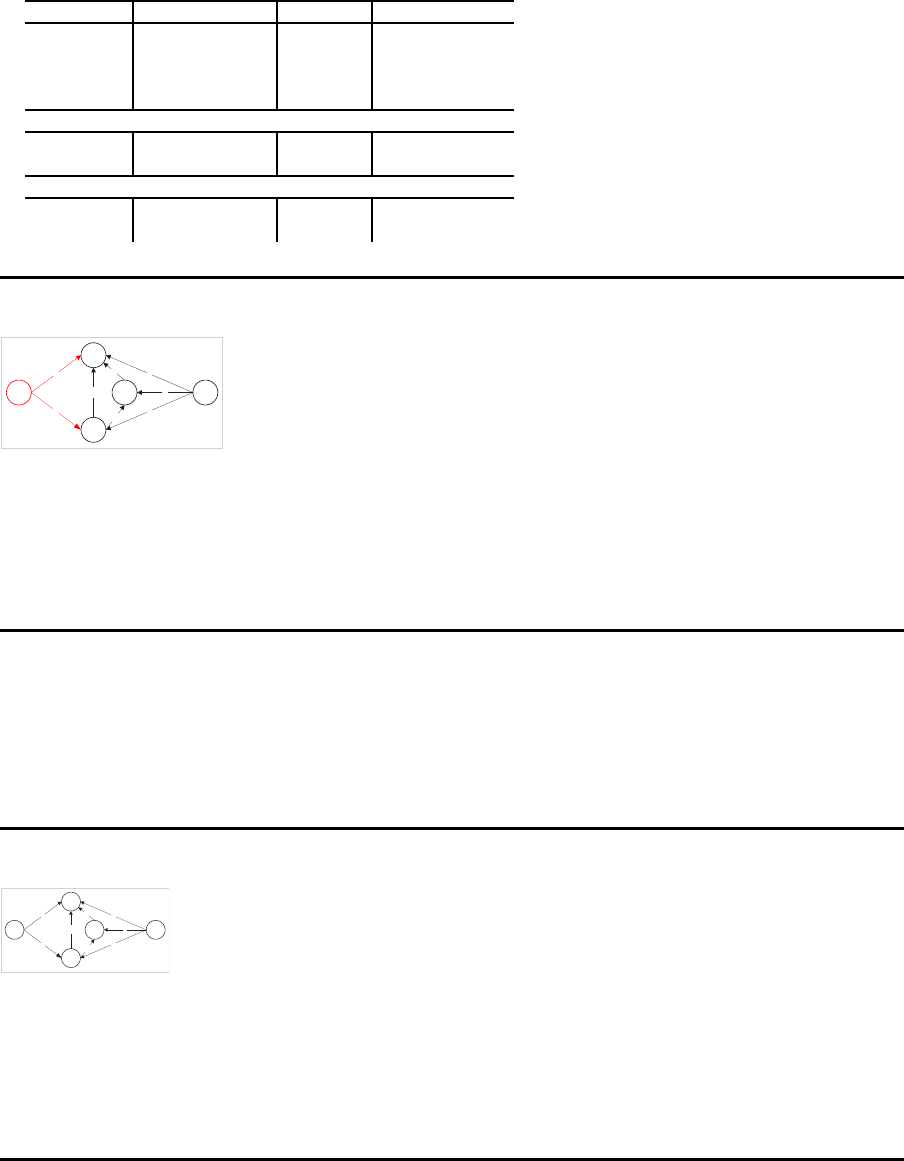
Erzeugnis P1
Position Sachnummer Menge Bezeichnung
1 E1 3 Einzelteil
2 B1 2 Baugruppe
3
B2 1 Baugruppe
4 E2 2 Einzelteil
Erzeugnis B1
1 B2 2 Baugruppe
2 E2 4 Einzelteil
Erzeugnis B2
1 E1 5 Einzelteil
2 E2 2 Einzelteil
Lineares Gleichungssystem
P1
E1 B1
B2
E2
3
2
1
2
4
5 2
2
y
E1
= 5 ·r
B2
+ 3 · r
P 1
r
k
Gesamtbedarf des Erzeugnisses k
y
k
Sekund¨arbedarf des Erzeugnisses k
Lineares Gleichungssystem II
y
k
=
X
j∈N
k
a
kj
· r
j
k = 1, 2, ..., K
Lineares Gleichungssystem III
P1
E1 B1
B2
E2
3
2
1
2
4
5 2
2
y
E1
= 0 · r
E1
+ 0 · r
E2
+ 0 · r
B1
+ 5 · r
B2
+ 3 · r
P 1
y
E2
= 0 · r
E1
+ 0 · r
E2
+ 4 · r
B1
+ 2 · r
B2
+ 2 · r
P 1
y
B1
= 0 · r
E1
+ 0 · r
E2
+ 0 · r
B1
+ 0 · r
B2
+ 2 · r
P 1
y
B2
= 0 · r
E1
+ 0 · r
E2
+ 2 · r
B1
+ 0 · r
B2
+ 1 · r
P 1
y
P 1
= 0 · r
E1
+ 0 · r
E2
+ 0 · r
B1
+ 0 · r
B2
+ 0 · r
P 1
Lineares Gleichungssystem
r
k
= y
k
+ d
k
k = 1, 2, . . . , K
53
r
k
=
X
j∈N
k
a
kj
· r
j
+ d
k
k = 1, 2, . . . , K
r
= A · r + d
r − A · r = d
r = (E − A)
−1
· d
v
kj
=
X
i∈N
k
a
ki
· v
ij
k 6= j
Vorgehe n sweise der B edarfsermittlung I
• Prim¨arbeda rf
• Bruttobedarf
Prim¨arbeda rf ( = direkt absatzbestimmter Bedarf)
+ Sekund¨arbedarf ( = abgeleiteter Bedarf)
+ prognostizierter Bedarf
+ Zusatzbedarf
= Bruttobedarf des Produkts k in Periode t, BRUTTO
kt
Vorgehe n sweise der B edarfsermittlung II
• disp onibler Lagerbestand
physischer Bestand
+ noch ausstehende Bestellungen
− reservierter Bestand
− Sicherheitsbestand
= disponibler Bestand des Produkts k in Periode t, DISPON
kt
NETTO
kt
= max {BRUTTO
kt
− DISPON
kt
, 0}
• Vorlaufverschiebung
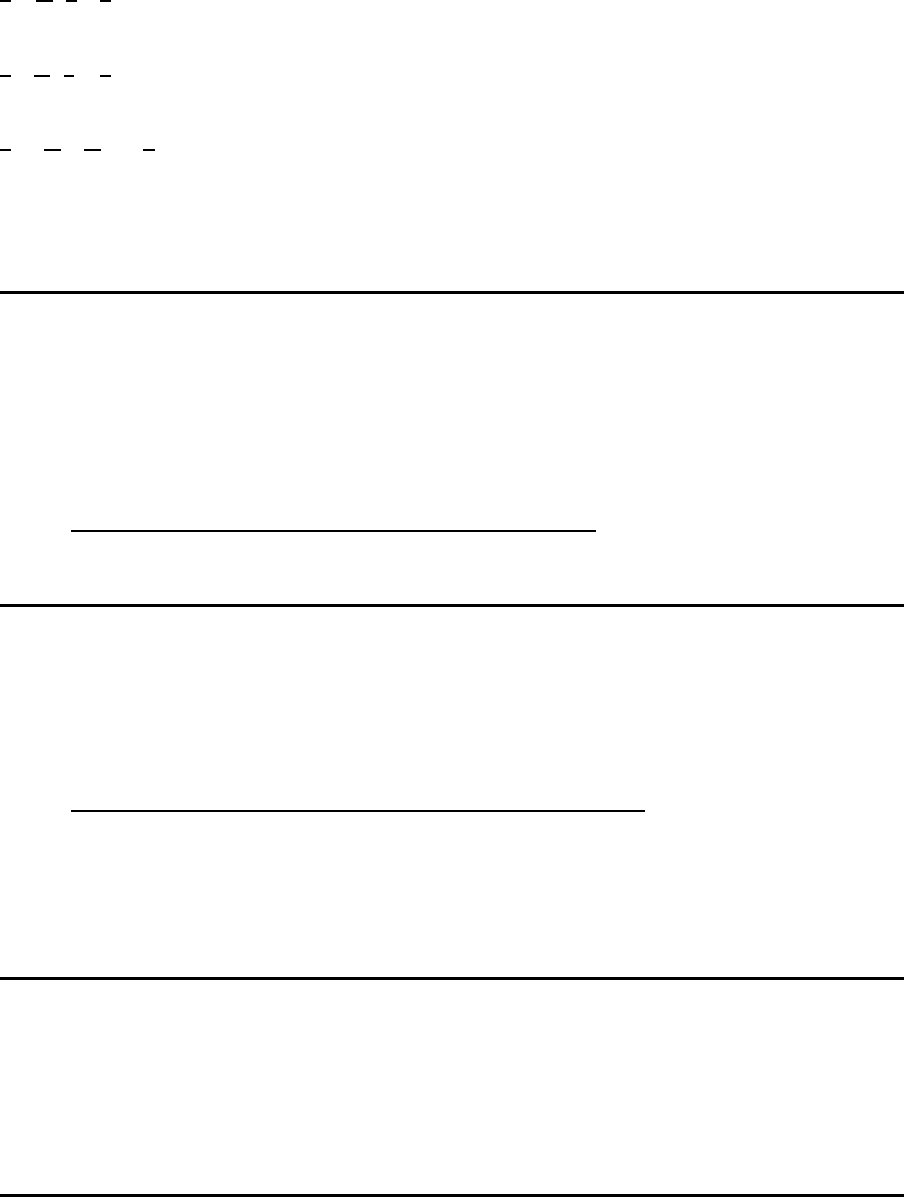
Dispositionsstufe
Definition
u
k
=
max
j∈N
k
{u
j
} + 1 N
k
6= ∅
0 N
k
= ∅
54
Dispositionsstufe I
P1
E1 B1
E3
1 4
1 2
E2
2
0
1
1
2
2
55

11.3 Dynamische Losgr¨oßenplanung – Das Problem
Losgr¨oßenplanung – Entscheidungsproblem
• Bestimme kostenminimale Losgr¨oßen
• unter Ber¨ucksichtigung
– periodenspez ifischer (dynamischer) Nachfragemengen
– periodenspez ifischer Produktionskapazit¨aten
– der Erzeugnis- und Prozeßstruktur
Optimierungsmodell
MLCLSP – Multi-Level Capacitated Lot Sizing Problem
MinimiereZ =
K
X
k=1
T
X
t=1
s
k
·γ
kt
+ h
k
·y
kt
u. B. d. R.
y
k,t−1
+ q
k,t−z
k
−
X
i∈N
k
a
ki
· q
it
− y
kt
= d
kt
k = 1, 2, . . . , K; t = 1, 2, . . . , T
X
k∈K
j
tb
k
·q
kt
+ tr
k
· γ
kt
≤ b
jt
j = 1, 2 , . . . , J; t = 1, 2, . . . , T
q
kt
− M · γ
kt
≤ 0
q
kt
≥ 0 k = 1, 2, . . . , K; t = 1, 2, . . . , T
y
kt
≥ 0 k = 1, 2, . . . , K; t = 1, 2, . . . , T
y
k0
= 0; y
kT
= 0 k = 1, 2, . . . , K
γ
kt
∈ {0, 1} k = 1, 2, . . . , K; t = 1, 2, . . . , T
56
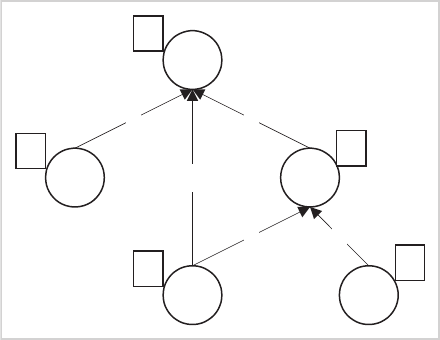
MLCLSP
Beispiel – Erzeugnis- und Prozeßstruktur
E1 P1
B1
B2
MLCLSP
Beispiel – L¨osung ohne Kapazit¨at s beschr¨ankungen, Nachfrage P1={10,10,30,15}
E1 P1
B1
B2
R¨ustvorg¨ange Produktionsmengen Lagerbest¨ande
Periode Periode Periode
Produkt 1 2 3 4 1 2 3 4 1 2 3 4
P1 1 – 1 – 20 – 45 – 10 – 15 –
B1
1 – – – 65 – – – 45 45 – –
B2
1 – – – 65 – – – 45 45 – –
E1
1 – – – 130 – – – – – – –
Kapazit¨atsbedarfe: 280 – 45 –
57
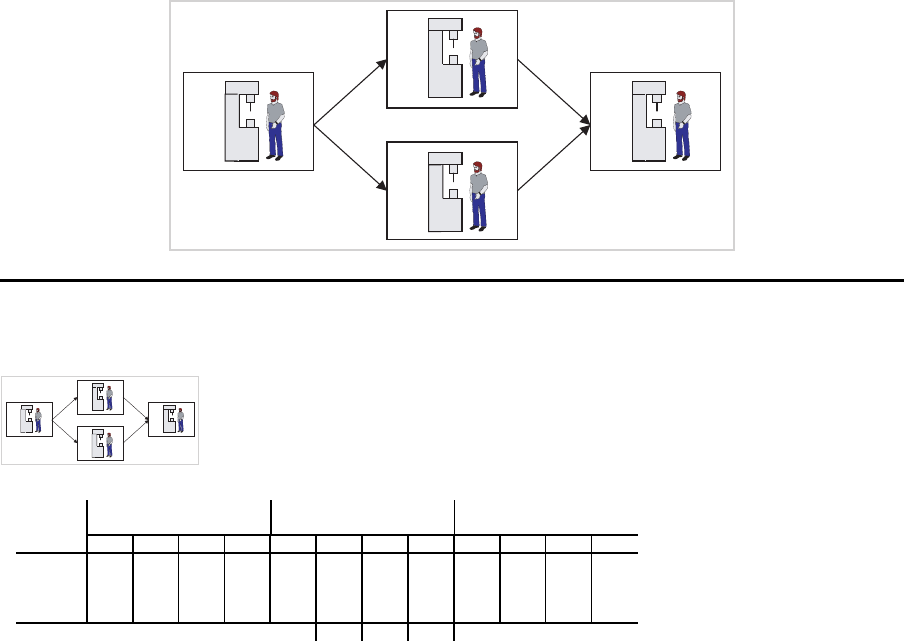
MLCLSP
Beispiel – Terminabweichun gen, Nachfrage P1={10,10,30,15}
E1
1 2 3 4
B1 B2 P1 P1
Verspätungen
Perioden
!
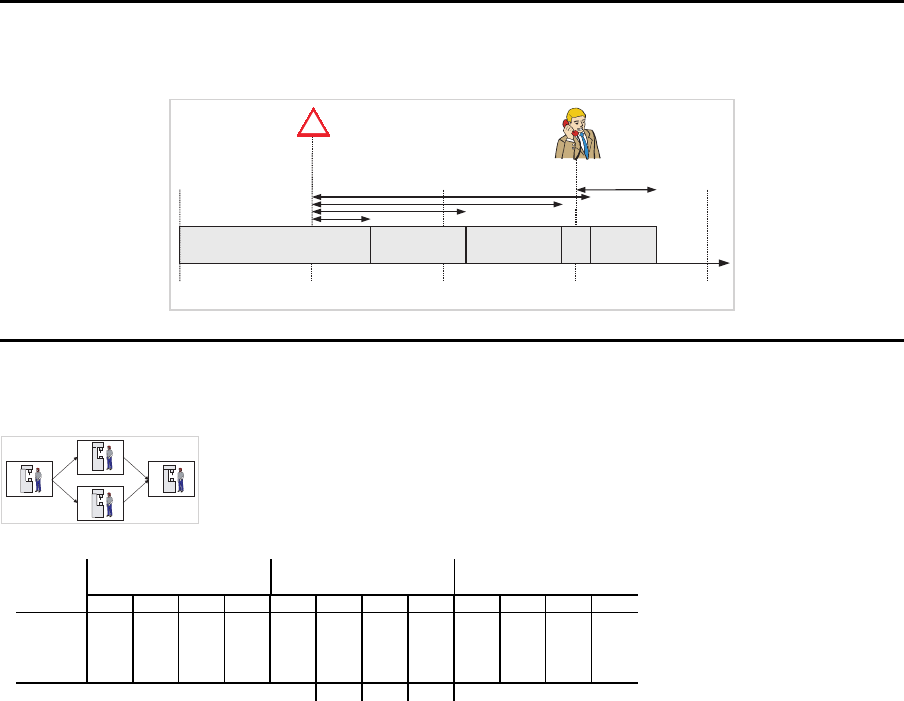
MLCLSP
Beispiel – L¨osung mit Kapazit¨ats beschr¨ankungen, Nachfrage P1={10,10,30,15}
E1 P1
B1
B2
R¨ustvorg¨ange Produktionsmengen Lagerbest¨ande
Periode Periode Periode
Produkt 1 2 3 4 1 2 3 4 1 2 3 4
P1 1 1 1 1 10 10 30 15 – – – –
B1
1 – 1 1 20 – 30 15 10 – – –
B2
1 – 1 1 20 – 30 15 10 – – –
E1
1 1 – 1 40 60 – 30 – 60 – –
Kapazit¨atsbedarfe: 90 70 90 75
58
11.4 Dynamische Losgr¨oßenplanung – Praxis
Reduktionsschritte des Losgr¨oßenproblems
Mehrstufiges Mehrprodukt-
Losgrößenproblem
mit beschränkten Kapazitäten
der Ressourcen
Mehrstufiges Mehrprodukt-
Losgrößenproblem
ohne Kapazitätsbeschränkungen
Mehrere unabhängig zu lösende
Einprodukt-Losgrößenprobleme
ohne Kapazitätsbeschränkungen
Vernachlässigung der
Kapazitätsbeschränkungen
Vernachlässigung der Beziehungen
zwischen den Erzeugnissen
Produkt 1
Produkt 2
Produkt K
...
Das dynami sche Einprodukt-Losg r¨oßenproblem
Annahmen
• T Perioden
• Anfangsbestand = 0
• keine Fehlmengen
• keine Kapazit¨ats beschr¨ankungen
• fixe R¨ust- bzw. Bestellkosten s
• Lagerkosten h
Modell SLULSP
Single-Level Uncapacitated Lot Sizing Problem
Minimiere Z =
T
X
t=1
h · y
t
+ s · γ
t
u. B. d. R.
y
t−1
+ q
t
− y
t
= d
t
t = 1, 2, . . . , T
q
t
− M · γ
t
≤ 0 t = 1, 2, . . . , T
q
t
≥ 0 t = 1, 2, . . . , T
y
t
≥ 0 t = 1, 2, . . . , T
59
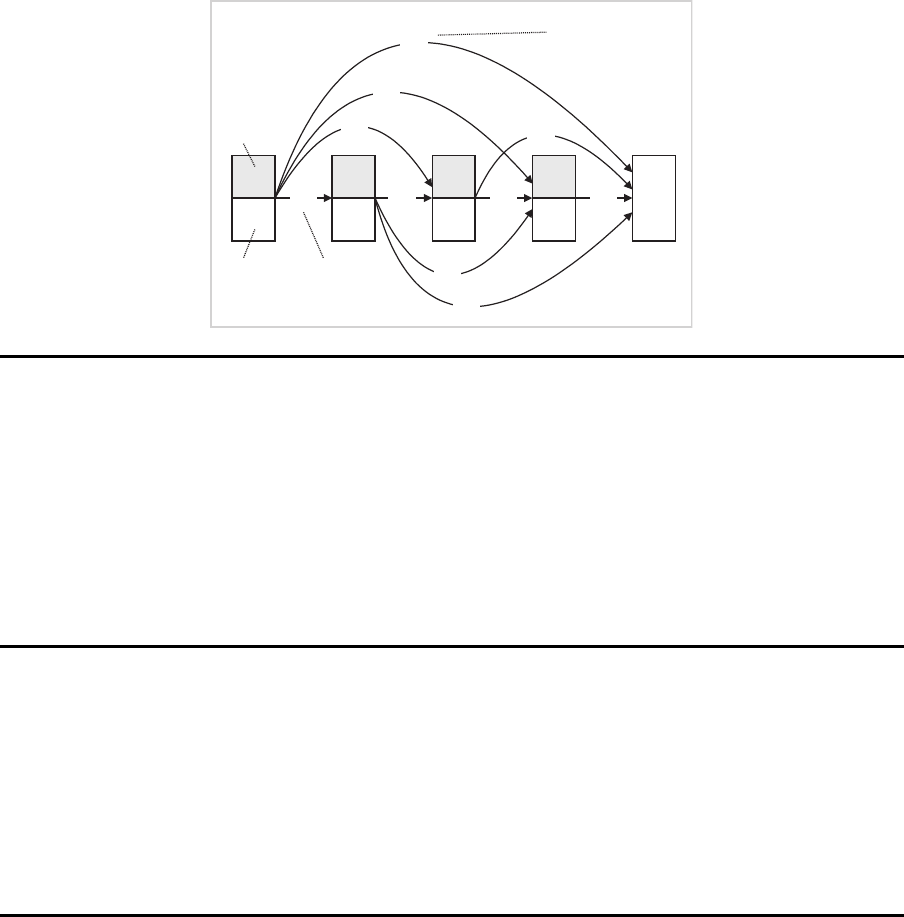
Alternative Modellierung
als K¨ur z este-Wege-Problem
1
10
2
10
3
30
4
15
E
100 100 100 100
140
220
380
560
160
340
Rüst- und
Lagerkosten
Rüstkosten
Periode
Bedarf
Exakte L¨osung des SLULSP
• Das SLULSP (Wagner-Whitin-Problem) kann exakt optimal gel¨ost werden.
• Der Rechenaufwand steigt quadratisch mit der Zahl der Perioden.
• In der Praxis se tzt man heuristische Verfahren zur L¨osung des SLULSP ein.
• Die heuristischen Ve rfahren greifen i. d. R. auf Optimalit¨atsbedingungen des klass ischen Losgr¨oßenmodells
bei konstantem Bedarf zur¨uck.
Klassisches Losgr¨oßenmodell - Annahmen
• kontinuierlicher und konstanter Bedarf: D (ME/ZE)
• R¨ustkosten: s (GE/R¨ustvorgang).
• Lagerkosten: h [GE/(ME·ZE)]
• Lagerzugang unendlich schnell
Klassisches Losgr¨oßenmodell
Bestandsentwicklung
60
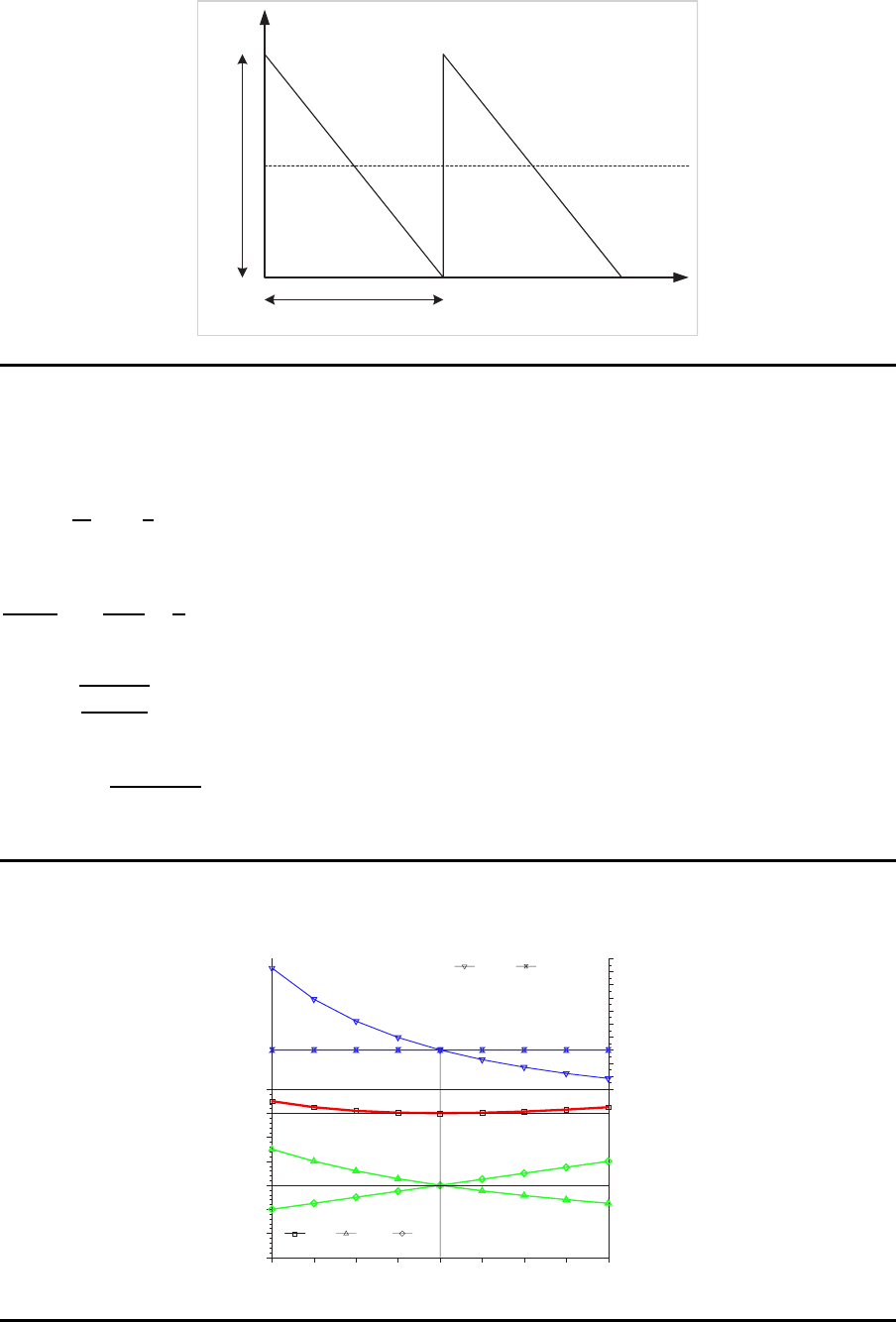
Zeit
durchschnittlicher
Lagerbestand
Losgröße q
Produktionszyklus
Klassisches Losgr¨oßenmodell
Optimale L¨osung
C (q) =
D
q
·s +
q
2
·h Zielfunktion
dC (q)
dq
= −
D · s
q
2
+
h
2
!
= 0 1. Ableitung nach q
q
opt
=
r
2 · D · s
h
optimale Losgr¨oße
C (q
opt
) =
√
2 · D · s · h minimale Kosten
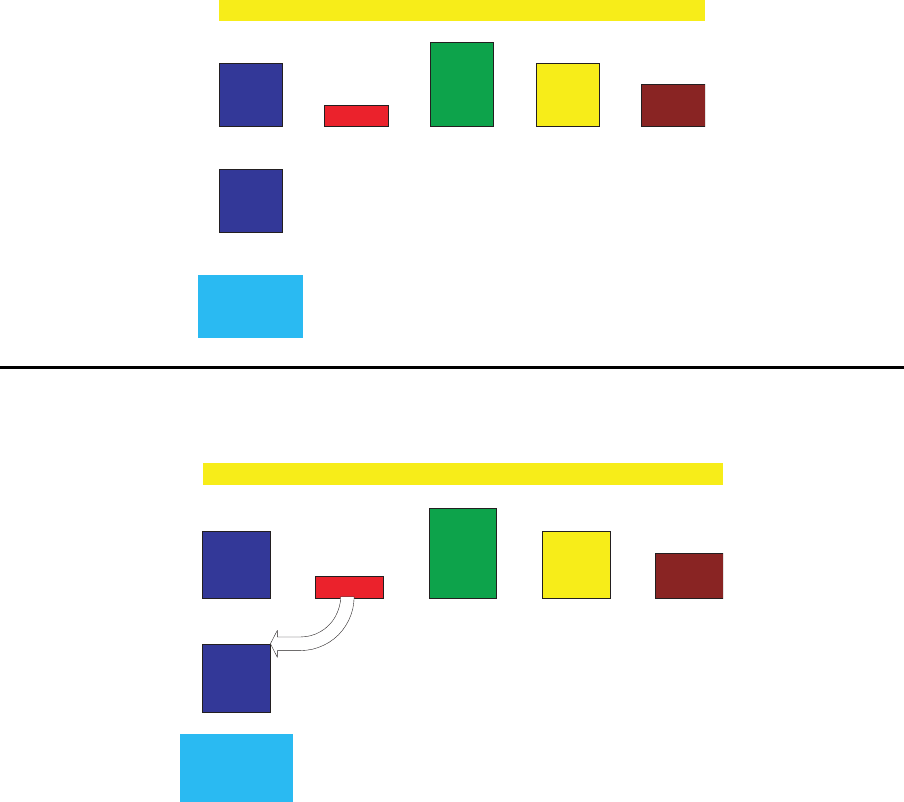
Klassisches Losgr¨oßenmodell
Verlauf der Zielfunktion
0
5
10
15
20
25
30
35
Gesamtkosten
Lager-, Rüst- und
0.010
0.015
0.020
0.025
0.030
0.035
0.040
0.045
0.050
0.055
0.060
Grenz- und
Durchschnittskosten
400 450 500 550 600 650 700 750 800
Losgröße
C(q) D·s/q q·h/2
D·s/q
2
h/2
Lagerkosten
Rüstkosten
Gesamtkosten
Grenz-Lagerkosten
Grenz-Rüstkosten
61
Dynamische Losgr¨oßenheuristiken
Vorgehensweise eines typischen heuristischen Verfahrens I
1
2
3
4
5
Nachfragezeitreihe
1
Losgröße
Periode 1
Dynamische Losgr¨oßenheuristiken
Vorgehensweise eines typischen heuristischen Verfahrens II
1
2
3
4
5
Nachfragezeitreihe
1
?
Losgröße
Periode 1
62
Dynamische Losgr¨oßenheuristiken
Vorgehensweise eines typischen heuristischen Verfahrens III
1
2
3
4
5
Nachfragezeitreihe
1
1
2
Losgröße
Periode 1
Dynamische Losgr¨oßenheuristiken
Vorgehensweise eines typischen heuristischen Verfahrens III
1
2
3
4
5
Nachfragezeitreihe
1
1
2
?
Losgröße
Periode 1
Dynamische Losgr¨oßenheuristiken
Vorgehensweise eines typischen heuristischen Verfahrens III
63
1
2
3
4
5
Nachfragezeitreihe
1
1
2
?
3
Losgröße
Periode 1
Losgröße
Periode 3
Silver-Meal-Verfahren
Kosten pro Periode, Produktion in τ, Bedarfsdeckung bis t
τ = 1 t = 3
l = 1 l = 2 l = 3
d
1
Produktion in τ ←− d
2
←− ←− d
3
c
τ t
=
s + h ·
t
P
l=τ
(l − τ ) · d
l
t − τ + 1
Silver-Meal-Verfahren
Beispiel
t
1 2 3 4 5 6
d
t
100 120 80 110 80 40
Silver-Meal-Verfahren
Beispiel
τ
t C
t
V
t
Bedarf t in τ pro-
duzieren?
1 1 c
11
=
250
1
= 250
∞ ja (250 ≤ ∞)
2 c
12
=
490
2
= 245
250 ja (245 ≤ 250)
3 c
13
=
810
3
= 270
245 nein (270 > 245)
Losgr¨o ße q
1
= 100 + 120 = 220
Groff-Ve rfahren I
s
t
−
s
t + 1
=
s
t · (t + 1)
t = 1, 2, ..., T − 1
64

d
t+1
2
·h t = 1, 2, ..., T − 1
Groff-Ve rfahren II
d
τ +j
2
·h ≤
s
j · (j + 1)
d
τ +j
·j · (j + 1) ≤ 2 ·
s
h
65