Losgrößenplanung unter stochastischen Bedingungen
In der betrieblichen Realität sind die Daten, insbesondere die Nachfragedaten, aber auch die Produktionsausbeute (yield) in den meisten Fällen nicht mit Sicherheit bekannt. In der Planungspraxis versucht man dies zu berücksichtigen, indem man bei der Nettobedarfsrechnung den verfügbaren Lagerbestand um einen sogenannten Sicherheitsbestand korrigiert und dann die Losgrößen mit einem Losgrößenalgorithmus für deterministischen Bedarf, z.B. dem heuristischen Silver-Meal-Verfahren oder auch mit einem exakten Verfahren bestimmt. Hierbei tritt regelmäßig das Problem auf, daß die richtige Höhe des Sicherheitsbestands unbekannt ist. Denn der Sicherheitsbestand hängt, wie wir aus der Lagerhaltungstheorie wissen, von der Länge der Wiederbeschaffungszeit und der Streuung der Nachfrage, d.h. von der Wahrscheinlichkeitsverteilung der Nachfragemenge im Risikozeitraum ab.
Ist auch die Ausbeute der Produktion unsicher, dann überlagern sich die Zufallseinflüsse. Siehe hierzu Kirste (2017).
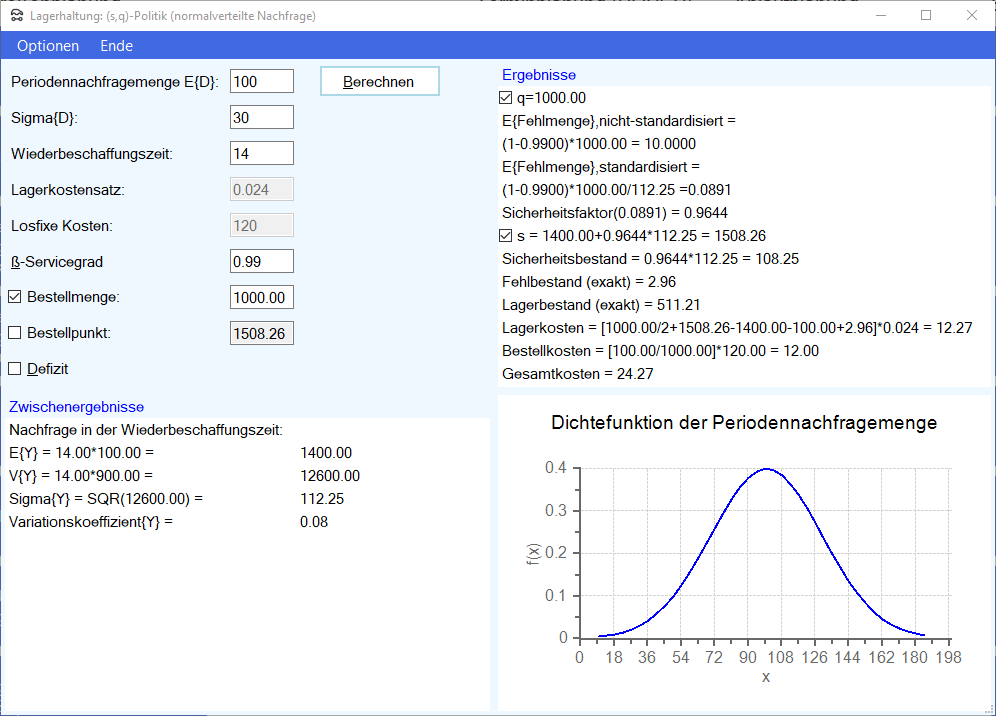
Darüberhinaus wird der Sicherheitsbestand von der Losgröße beeinflußt. In Abhängigkeit vom angestrebten Servicegrad kann es auch erforderlich sein, einen negativen Sicherheitsbestand einzuplanen. Nehmen wir z.B. an, es wird eine (s,q)-Lagerpolitik mit kontinuierlicher Bestandsüberwachung verfolgt. Die Periodennachfragemenge sei mit dem Mittelwert 100 und der Standardabweichung 30 normalverteilt. Die Wiederbeschaffungszeit ist deterministisch und beträgt 14 Tage. Bei einer Losgröße bzw. Bestellmenge von 1000 und einem angestrebten ß-Servicegrad von 99% beträgt der optimale Bestellpunkt $s=1508.25$. (Siehe hierzu Günther/Tempelmeier (2016) und die abgebildeten Berechnungen im Produktions-Management-Trainer).
Subtrahiert man vom Bestellpunkt $s=1508.25$ die erwartete Nachfragemenge in der Wiederbeschaffungszeit ($=14\cdot 100=1400$), dann erhält man den Sicherheitsbestand von 108.25.
Wird dagegen die Losgröße auf 5000 erhöht, dann ist der optimale Sicherheitsbestand mit -10.05 negativ. Prinzipiell gilt, je größer die Losgröße bzw. Bestellmenge ist, umso geringer ist der erforderliche Sicherheitsbestand.
Für die Bestimmung des Sicherheitsbestands muß man also die Losgröße kennen. Das bedeutet, sowohl die Losgröße als auch der Sicherheitsbestand müssen simultan festgelegt werden. In einem stochastischen Losgrößenmodell wird nun explizit berücksichtigt, daß die Höhe des Sicherheitsbestands nicht ein extern festgelegtes Datum ist, sondern unmittelbar von der Losgröße abhängt. In einem solchen Modell wird mit der Entscheidung über eine Losgröße in einer Periode gleichzeitig implizit der Sicherheitsbestand festgelegt, der zur Deckung der Unsicherheit bis zur nächsten Losauflage benötigt wird.
Anders als für den Fall deterministischer Nachfrage gibt es relativ wenige Ansätze zur Losgrößenplanung unter stochastischen Bedingungen. Die folgende Übersicht vermittelt einen ersten Eindruck:
| Stochastisches statisches einstufiges Mehrprodukt-Losgrößenproblem mit beschränkter Kapazität (SELSP) | Erweiterung des "Economic Lot Scheduling Problem" (ELSP) um die Berücksichtigung stochastischer Nachfragen |
| Stochastisches dynamisches Einprodukt-Losgrößenproblem ohne Kapazitätsbeschränkungen (SSIULSP) | Erweiterung des "Single-Item Uncapacitated Lot Sizing Problem" (SIULSP) um die Berücksichtigung stochastischer Nachfragen |
| Stochastisches dynamisches Einprodukt-Losgrößenproblem ohne Kapazitätsbeschränkungen (SSIULSP^Y) | Erweiterung des "Stochastic Single-Item Uncapacitated Lot Sizing Problem" (SSIULSP) um stochastische Ausbeute |
| Stochastisches dynamisches einstufiges Mehrprodukt-Losgrößenproblem mit beschränkter Kapazität (SCLSP) | Erweiterung des "Capacitated Lot Sizing Problem" (CLSP) um um die Berücksichtigung stochastischer Nachfragen |
Die stochastischen Losgrößenmodelle lassen sich noch danach unterscheiden, ob sie in der Zielfunktion Fehlbestandskosten berücksichtigen oder ob sie auf diese schwer quantifizierbaren Größen verzichten und statt dessen eine Servicegrad-Nebenbedingung berücksichtigen.
Siehe auch ...
- Produktions-Management-Trainer
- Zusammenhang zwischen Losgröße und Durchlaufzeit
- Erläuterung der Berechnungen zum Silver-Meal-Verfahren für stochastische Nachfrage (für das Beispiel aus Günther/Tempelmeier (2014), Abschnitt 12.5
Literatur
| Tempelmeier, H. (2020). Production Analytics. 6. Aufl., Norderstedt: Books on Demand. |
| Günther, H.-O. und Tempelmeier, H. (2020). Supply Chain Analytics - Operations Management und Logistik. 13. Aufl., Norderstedt: Books on Demand. |