EPQ: Klassisches Losgrößenmodell
Das klassische Losgrößenmodell ist vermutlich das am häufigsten in der Praxis eingesetzte Optimierungsmodell zur Losgrößenplanung.
Annahmen:
-
ein Produkt
-
stationäre Nachfragemenge $D$
-
endliche Produktionsgeschwindigkeit $p$
-
eine Ressource mit unbegrenzter Kapazität (d.h. die Ressource wird überhaupt nicht betrachtet)
Mit einem Lagerkostensatz $h$ und einem Rüstkostensatz $s$ sowie $\rho=\frac{p}{D}$ erhält man die durchschnittlichen Rüst- und Lagerkosten pro Periode. Die Zielfunktion des Optimierungsmodells lautet dann:
$Minimiere\; C\left( q \right)= h\cdot \frac{q}{2}\cdot \left( {1-\rho \right)} + s \cdot \frac{D}{q}$
Die optimale Losgröße $q_{opt}$ findet man durch Bildung der ersten Ableitung der Zielfunktion nach $q$. Setze man diese gleich Null, dann erhält man:
$\frac{dC\left( q \right)}{dq}=\frac{h}{2} \cdot (1-\rho) -\frac{D\cdot s}{q^2} \stackrel{!}{=} 0$
Daraus ergibt sich dann die optimale Losgröße:
$q_{opt} = \left({\frac{2\cdot s \cdot D}{h \cdot (1-\rho)}}\right)^\frac12 \quad$ (optimale Losgröße)
Die optimale Losgröße unterscheidet sich von der klassischen optimalen Bestellmenge,
$q_{opt} = \left({\frac{2\cdot s \cdot D}{h}}\right)^\frac12 \quad$ (optimale Bestellmenge)
nur durch den Einfluß der endlichen Produktionsgeschwindigkeit $p$. Da $p$ größer als Null ist, ist der maximale Lagerbestand nicht $q/2$, sondern nur $b_{max} = q \cdot (1-\rho)$. Eine Erhöhung der Losgröße führt also zu einem geringeren Anstieg der Lagerkosten als im Modell der klassischen Bestellmenge. Das wirkt genauso wie ein entsprechend reduzierter Lagerkostensatz. (siehe Günther/Tempelmeier (2014))
In der Formulierung dieses Optimierungsmodells hat die Ressource eine unbegrenzte Kapazität (bzw. die Kapazität wird überhaupt nicht erfaßt). In der Realität entsteht allerdings nur dann ein Losgrößenproblem, wenn die Kapazität beschränkt ist. Andernfalls könnte man ja jede auch noch so kleine Bedarfsmenge problemlos "just in time" produzieren. Man versucht nun, durch die Vorgabe von Rüstkosten die Häufigkeit des Rüstens zu beeinflussen. Aber: Um die optimale Losgröße bestimmen zu können, muß man die Rüstkosten kennen. Je höher diese sind, umso größer ist auch die optimale Losgröße.
Setzt man das klassische Losgrößenmodell zur Bestimmung der Losgrößen für mehrere Produkte ein, die auf einer Maschine nacheinander produziert werden, dann sind die ermittelten Losgrößen i.d.R. nicht zulässig, da es zu Überlagerungen der Produktionszeiträume der verschiedenen Produkte kommt. Dies zeigt das folgende einfache Beispiel. Wir betrachten 5 Produkte mit identischen Bedarfsraten (10), Produktionsraten (60), Rüstzeiten (1), Rüstkosten (20) und Lagerkostensätzen (0.001). Alle Produkte werden auf derselben Maschine produziert. Setzt man die klassische Losgrößenformel ein, dann erhält man für jedes Produkt die "optimale" Losgröße 692.82. Erzeugt man mit diesen Losgrößen nun einen Produktionsplan, dann sieht der wie folgt aus:
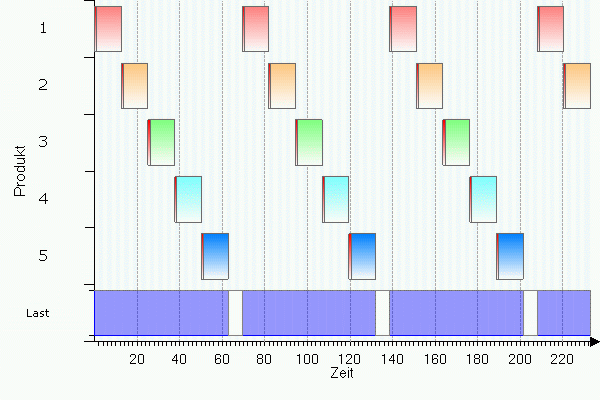
Es sind drei aufeinanderfolgende Produktionszyklen dargestellt. Die schmalen roten Balken stellen die Rüstzeiten dar, gefolgt von den Balken, die die Produktion beschreiben. Die Belastung der Maschine ist unten angezeigt. Wegen der hohen Rüstkosten sind die Losgrößen so groß, daß nach Abschluß der Produktion des letzten Produkts (5) noch eine Leerzeit verstreicht, bis mit dem zweiten Produktionszyklus begonnen wird.
Mit den angegebenen (unrealistischen) Daten ist dieser Produktionsplan zulässig. Eine geringfügige Datenänderung ergibt ein anderes Bild. Wir senken die Rüstkosten für Produkt 1 auf 10. Der Produktionsplan sieht dann so aus:
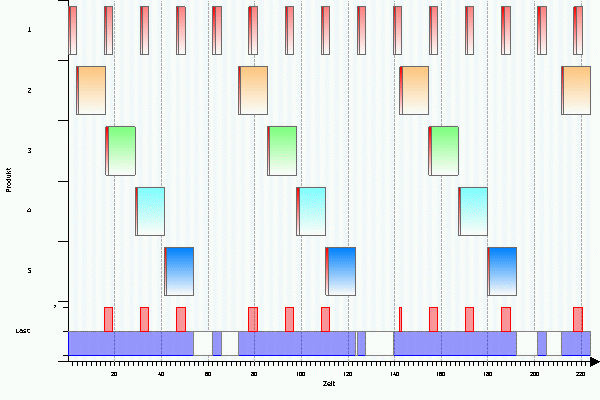
Man erkennt, daß es zu Überlagerungen der Produktionszeiträume auf der Maschine kommt. Die Folge sind Überlastungen der Maschine (rote Balken). Ein solcher Produktionsplan ist nicht machbar, also unzulässig. Eine Verschiebung der Produktionsaufträge, die die Überlastung der Maschine verursachen, in andere Perioden ist nicht möglich, da dann der regelmäßige Auf- und Abbau des Lagerbestands gestört wird und der Bestand für mindestens ein Produkt erschöpft ist, bevor mit seiner Produktion wieder begonnen werden kann.
Für das Beispiel mit realistischen Produktdaten aus Günther/Tempelmeier (2012) ergibt sich folgender nicht zulässiger Produktionsplan:
Auch hier wird die Ressource in einigen Zeitintervallen mehrfach belegt. Diese "optimale" Plan ist somit nicht machbar.
Diese einfachen Beispiele zeigen, daß das klassische Losgrößenmodell für die Erzeugung von machbaren Produktionsplänen, die die Grundlage für die tatsächlichen Produktionsabläufe sein sollen, ungeeignet ist. Ein machbarer Produktionsplan kann nur dann erzeugt werden, wenn simultan zur Losgrößenplanung auch eine Entscheidung über die Produktionsreihenfolge der Lose auf der Maschine getroffen wird.
Geht man weiterhin von stationärer Nachfrage aus, dann kann hierzu das Economic Lot Scheduling (ELSP) eingesetzt werden. Für die Unterstützung von operativen Entscheidungen wird man in den meisten Fällen jedoch Losgrößenmodelle anwenden müssen, die neben der Berücksichtigung der Kapazität der Ressource auch in der Lage sind, dynamischen Bedarf zu erfassen.
Siehe auch ...
- Produktions-Management-Trainer, Modul Losgrößen und Reihenfolgen (ELSP)
Literatur
| Günther, H.-O. und Tempelmeier, H. (2020). Supply Chain Analytics - Operations Management und Logistik. 13. Aufl., Norderstedt: Books on Demand. |
| Tempelmeier, H. (2020), Analytics in Supply Chain Management und Produktion - Übungen und Mini-Fallstudien. 7. Aufl., Norderstedt: Books on Demand. |