PLSP: Proportional Lotsizing and Scheduling Problem
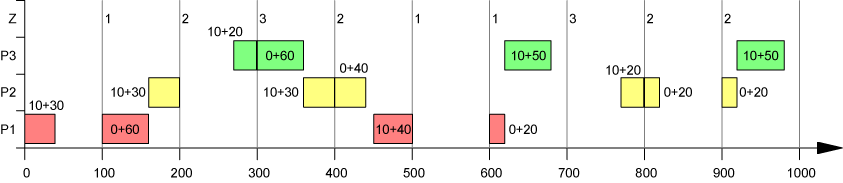
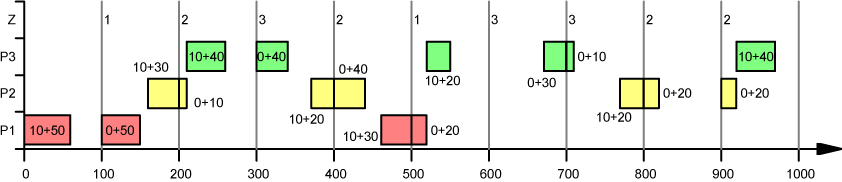
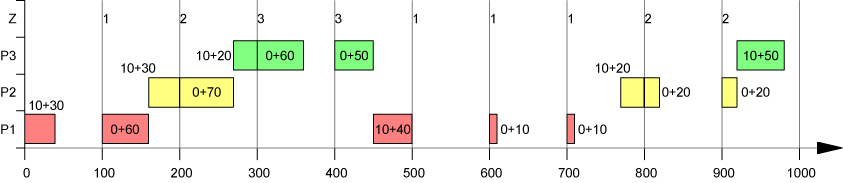
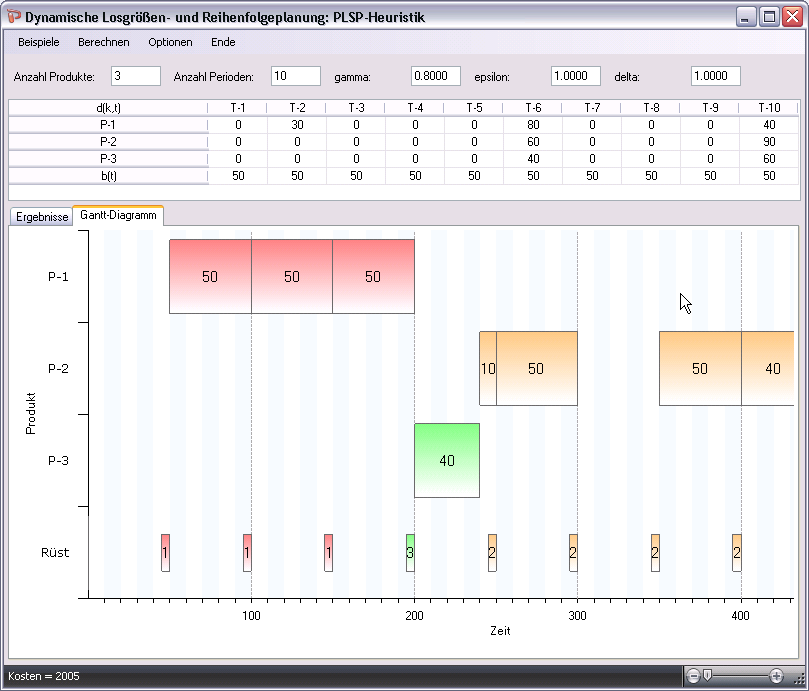
Dieses Modell geht von sehr kurzen Perioden aus (small-bucket Modell) und ermöglicht, falls die Kapazität einer Periode nicht voll durch die Produktion eines Produktes verbraucht wird, die Produktion eines zweiten Produktes. Die Grundbedingung des PLSP in seiner ursprünglichen Form lautet: In jeder Periode darf höchstens ein Produktwechsel erfolgen. Das PLSP soll den Fall modellieren, bei dem ein Los über mehrere Perioden hinweg produziert wird. Rüstkosten fallen nur einmal zu Beginn der Produktion mit der Vorbereitung der Ressource für das betreffende Produkt an. Das muß nicht die Produktionsperiode sein, in der mit der Produktion begonnen wird, sondern kann u.U. auch schon vorher (Ende der Vorperiode) passieren. Neben den üblichen (binären) Rüstvariablen benötigt man eine zusätzliche Variable, die den Rüstzustand der Ressource am Ende einer Periode wiedergibt. Eine PLSP-Lösung determiniert einen genau definierten Produktionsablauf mit fixierten Produktionsstart- und endterminen
Annahmen:
- mehrere Produkte
- dynamische Nachfragemengen
- eine Maschine
- endliche Produktionsgeschwindigkeit
- in einer Periode kann höchstens ein Produktwechsel erfolgen ("small bucket"-Modell)
- Übernahme eines Rüstzustandes aus der Vorperiode
Die mathematische Formulierung lautet:
$\begin{eqnarray} \mathrm{Minimiere } Z=\displaystyle{\sum_{k=1}^K \sum_{t=1}^T \left(s_k\cdot \gamma_{kt}+ h_k\cdot y_{kt} \right)} \end{eqnarray}$
unter den Nebenbedingungen
$y_{k,t-1}+q_{kt}-y_{kt}=d_{kt} \qquad{k=1,2,...,K; t=1,2,...,T}$
$\displaystyle{\sum_{k=1}^K} \left( tb_{k}\cdot q_{kt} + tr_{k}\cdot \gamma_{kt} \right) \leq b_{t} \qquad{t=1,2,...,T}$
$\displaystyle{\sum_{k=1}^K} z_{kt} = 1 \qquad {t=1,2,...,T}$
$\gamma_{kt} \geq z_{kt} - z_{k,t-1} \qquad{k=1,2,...,K; t=1,2,...,T}$
$q_{kt} \leq M\cdot \left( z_{k,t-1} + z_{kt} \right) \qquad {k=1,2,...,K; t=1,2,...,T}$
$z_{k0} = 0\qquad{k=1,2,...,K}$
$q_{kt}, y_{kt}\geq 0\qquad{k=1,2,...,K; t=1,2,...,T}$
$z_{kt}\in \{0,1\} \qquad{k=1,2,...,K; t=1,2,...,T}$
$\gamma_{kt}\in \{0,1\} \qquad{k=1,2,...,K; t=1,2,...,T}$
Symbole:
| $t$ | Periodenindex |
| $k$ | Produktindex |
| $d_{kt}$ | Primärbedarf des Produkts $k$ in Periode $t$ |
| $tb_{k}$ | Produktionszeit pro ME des Produkts $k$ |
| $tr_{k}$ | Rüstzeit für Produkt $k$ |
| $b_{t}$ | Kapazität der Ressource in Periode $t$ = Periodenlänge |
| $q_{kt}$ | Produktionsmenge des Produkts $k$ in Periode $t$ |
| $y_{kt}$ | Lagerbestand des Produkts $k$ am Ende der Periode $t$ |
| $\gamma_{kt}\quad$ | binäre Rüstvariable für Produkt $k$ in Periode $t$ |
| $z_{kt}$ | binäre Variable, die anzeigt, ob die Ressource am Ende der Periode $t$ für Produkt $k$ gerüstet ist |