Aggregierte Gesamtplanung: Modell 4 (Mehrstufige Produktion)
Es gelten alle Annahmen von Modell 1.
Jetzt wird zusätzlich angenommen, daß die Menge aller Produkte in Endprodukte und Vorprodukte aufgeteilt ist, die in unterschiedlichen Fabriken hergestellt werden. So kann z.B. eine Fabrik in Hamburg und die andere in München stehen. Die Endprodukte werden in Hamburg und die Vorprodukte werden in München produziert. Alle Vorprodukte müssen somit von München nach Hamburg transportiert werden. In dieser Situation hängt der optimale Produktionsplan in Hamburg u.a. auch von den verfügbaren Kapazitäten in München ab.
Grundannahmen des Modells 1:
- Mehrere (End-)Produktgruppen $k\in {K}_s$.
- $T$ Perioden (Wochen, Monate, Quartale).
- Produkt- und periodenspezifische Nachfragemengen.
- Keine explizite Modellierung der Nachfrager.
- Der Distributionsprozeß wird nicht abgebildet.
Zusätzliche Annnahmen des Modells 4:
- Mehrere Fabriken, wobei einige Fabriken Vorprodukte und andere Fabriken endprodukte herstellen.
- Jeder Fabrik, die Endprodukte herstellt, ist ein regionaler Absatzmarkt zugeordnet, der ausschließlich durch die Fabrik beliefert wird.
- Es bestehen Input-Output-Beziehungen zwischen den Vor- und Endprodukten, die durch eine Direktbedarfsmatrix $Q$ abgebildet werden. Das Element $q_{jk}$ gibt dann die Menge des Vorprodukts $j$ an, die zur Herstellung einer ME des Endprodukts $k$ benötigt wird.
- Zielfunktion: Lagerkosten, Überstundenkosten
Das Modell lautet:
$\mathrm{minimiere }Z = \displaystyle{ \sum_{s \in {S}} \sum_{k \in {K}_s} \sum_{t = 1}^T} { l_{sk} \cdot L_{skt}} + \displaystyle{\sum_{s \in {S}} \sum_{t = 1}^T } {u_{st} \cdot U_{st} $
unter den Nebenbedingungen
$L_{sk,t - 1} + X_{skt} - $ $ \displaystyle{\sum_{j \in {K}} q_{kj} \cdot X_{sjt} } $ $ - L_{skt} = d_{skt} \qquad s \in {S}; k\in {K}_s; t=1,2,...,T $
$\displaystyle{\sum_{k \in {K}_s}} b_{sk} \cdot X_{skt} \leq C_{st,\max } \qquad s \in {S}; t=1,2,...,T$
$\displaystyle{ \sum_{k \in {K}_s} } a_{sk} \cdot X_{skt} - U_{st} \leq N_{st,\max } \qquad s \in {S}; t=1,2,...,T $
$U_{st} \leq U_{st,\max } \qquad s \in {S}; t=1,2,...,T
$X_{skt}, L_{skt}, U_{st} \ge 0 \qquad s \in {S}; k\in {K}_s; t=1,2,...,T $
Symbole:
| $a_{sk}$ | Produktionskoeffizient für Produkttyp $k$ in bezug auf die personelle Kapazität am Standort $s$ |
| $b_{sk}$ | Produktionskoeffizient für Produkttyp $k$ in bezug auf die technische Kapazität am Standort $s$ |
| $C_{st,\max}$ | technische Kapazität in Periode $t$ am Standort $s$ |
| $d_{skt}$ | Nachfrage für Produkttyp $k$ in Periode $t$ am Standort $s$ |
| $K_{s}$ | Indexmenge der Produkte, die am Standort $s$ produziert werden |
| $s$ | Index der Fabriken (in Modell nur eine Fabrik $s=1$) |
| ${S}$ | Indexmenge der Fabriken |
| $N_{st,\max}$ | personelle Kapazität am Standort $s$ in Periode $t$ |
| $U_{st,\max}$ | maximale personelle Zusatzkapazität am Standort $s$ in Periode $t$ |
| $u_{st}$ | Kosten für eine Einheit zusätzlicher personeller Kapazität am Standort $s$ |
| $L_{skt}$ | Lagerbestand für Produkttyp $k$ am Standort $s$ am Ende von Periode $t$ |
| $U{st}$ | genutzte personelle Zusatzkapazität am Standort $s$ in Periode $t$ |
| $X_{skt}$ | Produktionsmenge von Produkttyp $k$ am Standort $s$ in Periode $t$ |
| $q_{kj}$ | Anzahl ME des Endprodukts $k$, die zur Herstellung einer Einheit des Endprodukts $j$ benötigt werden |
Die Zielfunktion des Modells bildet den Zielkonflikt zwischen den Lagerkosten und den Kosten für Zusatzkapazität (flexible Produktionskapazität) ab. Dabei wird simultan ein optimaler Abgleich aller Lager- und Überstundenkosten an allen Standorten erreicht.
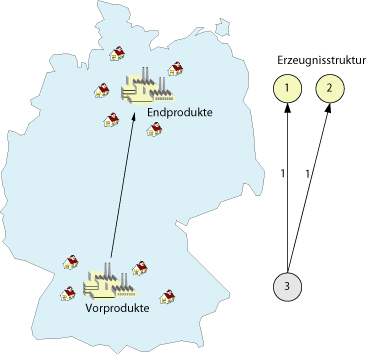
Beispiel: 3 Produkte, davon 1 Vorprodukt und 2 Endprodukte, 6 Perioden
Die Struktur des Problems zeigt das folgende Bild:
| Kostendaten: |
Fabrik 1 |
||
Produkt 1 |
||
Lagerkostensatz |
4.00 |
|
Personalbedarf pro ME |
1.00 |
|
Kapazitätsbedarf pro ME |
0.50 |
|
Lager-Anfangsbestand |
20.00 |
|
Lager-Mindestbestand |
0.00 |
|
Produkt 2 |
||
Lagerkostensatz |
4.00 |
|
Personalbedarf pro ME |
0.50 |
|
Kapazitätsbedarf pro ME |
1.00 |
|
Lager-Anfangsbestand |
10.00 |
|
Lager-Mindestbestand |
0.00 |
|
Sonstiges |
||
Lager-Maximalbestand |
9999.00 |
|
Überstundenlohnsatz |
5.00 |
Fabrik 2 |
Produkt 3 |
||
Lagerkostensatz |
3.00 |
|
Produktionskostensatz |
0.00 |
|
Personalbedarf pro ME |
1.00 |
|
Kapazitätsbedarf pro ME |
1.00 |
|
Lager-Anfangsbestand |
0.00 |
|
Lager-Mindestbestand |
0.00 |
|
Sonstiges |
||
Lager-Maximalbestand |
20.00 |
|
Überstundenlohnsatz |
4.00 |
| Kapazitäten und Nachfragedaten: |
Fabrik 1:
Periode |
Cmax |
Nmax |
Umax |
Nachfrage 1 |
Nachfrage 2 |
1 |
200.0 |
160.0 |
50.0 |
60.0 |
100.0 |
2 |
200.0 |
160.0 |
50.0 |
90.0 |
110.0 |
3 |
200.0 |
160.0 |
50.0 |
110.0 |
90.0 |
4 |
200.0 |
160.0 |
50.0 |
100.0 |
130.0 |
5 |
200.0 |
160.0 |
50.0 |
80.0 |
160.0 |
6 |
200.0 |
160.0 |
50.0 |
70.0 |
70.0 |
7 |
200.0 |
160.0 |
50.0 |
110.0 |
70.0 |
8 |
200.0 |
160.0 |
50.0 |
130.0 |
150.0 |
Fabrik 2:
Periode |
Cmax |
Nmax |
Umax |
1 |
300.0 |
320.0 |
100.0 |
2 |
300.0 |
320.0 |
100.0 |
3 |
300.0 |
320.0 |
100.0 |
4 |
200.0 |
320.0 |
100.0 |
5 |
300.0 |
320.0 |
100.0 |
6 |
100.0 |
320.0 |
100.0 |
7 |
300.0 |
320.0 |
100.0 |
8 |
300.0 |
320.0 |
100.0 |
Optimale Lösung:
Fabrik 1:
Periode |
Prod.-Menge 1 |
Prod.-Menge 2 |
Bestand 1 |
Bestand 2 |
0 |
20 |
10 |
||
1 |
40 |
90 |
- |
- |
2 |
95 |
110 |
5 |
- |
3 |
105 |
110 |
- |
20 |
4 |
100 |
120 |
- |
10 |
5 |
100 |
150 |
20 |
- |
6 |
50 |
70 |
- |
- |
7 |
120 |
80 |
10 |
10 |
8 |
120 |
140 |
- |
- |
Periode |
Technische Belastung |
Personelle Belastung |
Überstunden |
|
1 |
110 |
85 |
- |
|
2 |
157.5 |
150 |
- |
|
3 |
162.5 |
160 |
- |
|
4 |
170 |
160 |
- |
|
5 |
200 |
160 |
15 |
|
6 |
95 |
85 |
- |
|
7 |
140 |
160 |
- |
|
8 |
200 |
160 |
30 |
Fabrik 2:
Periode |
Prod.-Menge 3 |
Bestand 3 |
|
0 |
- |
||
1 |
130 |
- |
|
2 |
205 |
- |
|
3 |
235 |
20 |
|
4 |
200 |
- |
|
5 |
270 |
20 |
|
6 |
100 |
- |
|
7 |
200 |
- |
|
8 |
260 |
- |
|
Periode |
Technische Belastung |
Personelle Belastung |
Überstunden |
1 |
130 |
130 |
- |
2 |
205 |
205 |
- |
3 |
235 |
235 |
- |
4 |
200 |
200 |
- |
5 |
270 |
270 |
- |
6 |
100 |
100 |
- |
7 |
200 |
200 |
- |
8 |
260 |
260 |
- |
Siehe auch ...
- Produktions-Management-Trainer
- Modell 1
- Modell 2: Eine Fabrik, Fremlieferanten
- Modell 3: Mehrere Fabriken
Literatur
| Günther, H.-O. und Tempelmeier, H. (2020). Supply Chain Analytics - Operations Management und Logistik. 13. Aufl., Norderstedt: Books on Demand. |
| Tempelmeier, H. (2020), Production ANalytics. 6. Aufl., Norderstedt: Books on Demand. | Tempelmeier, H. (2020). Analytics in Supply Chain Management und Produktion - Übungen und Mini-Fallstudien. 7. Aufl., Norderstedt: Books on Demand. |