Wir betrachten ein 2-Stationen-System mit den Stationen (1,2) bzw. ($m,m+1$) und wollen die Produktionsrate $X(m,m+1)$ dieses Systems bestimmen. Dieses 2-Stationen-System kann auch als ein Subsystem eines längeren Fließproduktionssystem mit begrenzten Puffern betrachtet werden. Daher die Notation ($m,m+1$).
Zur Analyse eines solchen 2-Stationen-Systems stehen verschiedene Modelle zur Verfügung, die von den speziellen Eigenschaften des Systems abhängen. Es gibt u.a. Modelle für folgende Systemtypen:
- exponential-verteilte Bearbeitungszeiten, keine Störungen
- allgemein-verteilte Bearbeitungszeiten, keine Störungen
- deterministische Bearbeitungszeiten, an allen Stationen identisch, Störungen
- deterministische Bearbeitungszeiten, stationsspezifisch, Störungen
Im einfachsten Fall gehen wir von folgenden Annahmen aus:
- asynchroner Materialfluß
- an allen Stationen exponentialverteilte Bearbeitungszeiten
- keine Störungen
Für die betrachtete Situation geht man wie folgt vor. Wir bezeichnen mit $\lambda$ die Bearbeitungsrate der Station 1 und mit $\mu$ die Bearbeitungsrate der Station 2 des Subsystems. Die Station 1 ist niemals unbeschäftigt, da wir annehmen, daß immer genügend Rohmaterial vorhanden ist.
Gehen wir zunächst davon aus, daß die Größe des Puffers in dem
Subsystem gleich $c=0$ ist.In diesem Fall sieht das System so aus:
Ein Zustand wird beschrieben durch die Anzahl $n$ von Werkstücken in dem
Subsystem, die bereits an der Station 1, aber noch nicht
an Station 2 bearbeitet worden sind. Die Anzahl der Zustände hängt also davon ab, wie viele Werkstücke an
der Station 1 bereits bearbeitet worden sind, aber noch nicht die Station 2
passiert haben. Das sind
- $c$ Werkstücke im Puffer,
- 1 Werkstück an Station 2 in Bearbeitung und
- 1 Werkstück an Station 1, wenn diese blockiert wird,
also insgesamt $c+2$ Zustände. Hinzu kommt der Zustand, an dem kein Werkstück auf Station 2 wartet, diese also leer ist. D.h. die Anzahl der Zustände ist $c+3$. Ist die Pufferkapazität $c=0$, dann können folglich insgesamt 3 Zustände auftreten. Im vorliegenden Fall also:
$n$ |
Station 1 |
Puffer |
Station 2 |
0 |
arbeitet |
-- |
leer |
1 |
arbeitet |
-- |
arbeitet |
2 |
blockiert |
-- |
arbeitet |
Betrachten wir nun ein Subsystem mit zwei Pufferplätzen ($c=2$):
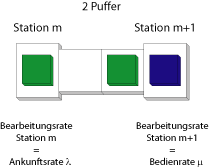
In diesem Fall gibt es $2+3=5$ Zustände, und zwar
$n$ |
Station 1 |
Puffer |
Station 2 |
0 |
arbeitet |
leer |
leer |
1 |
arbeitet |
leer |
arbeitet |
2 |
arbeitet |
1 Werkstück |
arbeitet |
3 |
arbeitet |
2 Werkstücke |
arbeitet |
4 |
blockiert |
3 Werkstücke |
arbeitet |
Das Gesamtsystem kann nicht leer sein, da Station 1 niemals unter Materialmangel leidet und somit immer entweder arbeitet oder blockiert ist. Zustandsveränderungen entstehen durch die Bearbeitungsende-Ereignisse an einer arbeitenden Station. Ist eine Station leer oder blockiert, dann tritt ein solches Ereignis nicht auf.
Wir stellen zunächst die Übergangsmatrix zwischen den Zuständen des Systems an zwei dicht beeinanderliegenden Zeitpunkten $t$ und $t+h$ auf. Die Zeitspanne $h$ sei so kurz, daß die Wahrscheinlichkeit dafür, daß mehr als eine Ankunft und/oder eine Fertigstellung eines Werkstücks an einer Station auftreten, vernachlässigbar gering ist. Es wird somit angenommen, daß in $h$ an jeder Station jeweils nur ein Ereignis auftritt.
Die folgende Matrix gibt die Wahrscheinlichkeiten der Zustandsänderungen für $c=0$ an.
| nach |
|||
von |
0 |
1 |
2 |
0 |
$(1-\lambda\cdot h)$: kein Bearbeitungsende an Station 1 |
$\lambda\cdot h$: Bearbeitungsende an Station 1 |
-- |
1 |
$(1-\lambda\cdot h)\cdot \mu\cdot h$: kein Bearbeitungsende an Station 1, Bearbeitungsende an Station 2 |
$(1-\lambda\cdot h)\cdot (1-\mu\cdot h)$: kein Bearbeitungsende an Station 1, kein Bearbeitungsende an Station 2 |
$\lambda\cdot h \cdot (1-\mu\cdot h)$: Bearbeitungsende an Station 1, kein Bearbeitungsende an Station 2 |
2 |
-- |
$\mu\cdot h$: Bearbeitungsende an Station 2 |
$(1-\mu\cdot h)$: kein Bearbeitungsende an Station 2 |
Graphisch sieht das so aus:
Für $c=2$ Pufferplätze ergibt sich folgende Übergangsmatrix.
nach |
|||||
| von | 0 | 1 | 2 | 3 | 4 |
0 |
$(1-\lambda\cdot h)$ | $\lambda\cdot h$ | |||
1 |
$(1-\lambda\cdot h)\cdot \mu\cdot h$ | $(1-\lambda\cdot h)\cdot (1-\mu\cdot h)$ | $\lambda\cdot h \cdot (1-\mu\cdot h)$ | ||
2 |
$(1-\lambda\cdot h)\cdot \mu\cdot h$
|
$(1-\lambda\cdot h)\cdot (1-\mu\cdot h)$ | $\lambda\cdot h \cdot (1-\mu\cdot h)$ | ||
3 |
$(1-\lambda\cdot h)\cdot \mu\cdot h$
|
$(1-\lambda\cdot h)\cdot (1-\mu\cdot h)$ | $\lambda\cdot h \cdot (1-\mu\cdot h)$ | ||
4 |
$\mu\cdot h$ |
$(1-\mu\cdot h)$ | |||
Das folgende Bild zeigt den Übergangsgraphen:
Zur Bestimmung der Zustandswahrscheinlichkeiten zum Zeitpunkt $t+h$, $P_j(t+h)$, gewichtet man die Wahrscheinlichkeiten aller Zustände zum Zeitpunkt $t$, $P_i(t)$, die zum Zustand $P_j(t+h)$ im Zeitpunkt $t+h$ führen können, mit den jeweiligen Übergangswahrscheinlichkeiten $u_{ij}$ und bildet die Summe. Bei $n$ möglichen Zuständen erhält man dann $n$ Gleichungen der folgenden Form:
$P_j(t+h) = u_{1j}·P_1(t) + u_{2j}·P_2(t) + \ldots + u_{nj}·P_n(t)$
Für den Fall $c=0$ erhält man z.B.:
$ P_0(t+h) = (1-\lambda\cdot h)\cdot P_0(t) + (1-\lambda\cdot h)\cdot \mu\cdot h\cdot P_1(t) $ (I)
$ P_1(t+h) = \lambda\cdot h\cdot P_0(t) + (1-\lambda\cdot h)\cdot (1-\mu\cdot h) \cdot P_1(t) + \mu \cdot h \cdot P_2$
$ P_2(t+h) = \lambda\cdot h\cdot (1-\mu\cdot h) \cdot P_1(t) + (1-\mu \cdot h) \cdot P_2$
Die weiteren Berechnungen werden anhand Gleichung (I) demonstriert.
Ausmultiplizieren
$ P_0(t+h) = P_0(t) - \lambda\cdot h \cdot P_0(t) + \mu\cdot h\cdot P_1(t) - \lambda\cdot h \cdot \mu \cdot h\cdot P_1(t) $ (Ia)
Umformen und Vernachlässigung aller $h^2$-Terme:
$ P_0(t+h) - P_0(t) = - \lambda\cdot h \cdot P_0(t) + \mu\cdot h\cdot P_1(t) $ (Ib)
Division durch $h$:
$ \frac{P_0(t+h) - P_0(t)}{h} = - \lambda \cdot P_0(t) + \mu\cdot P_1(t) $ (Ic)
Die stationären Zustandswahrscheinlichkeiten $P_j$ erhält man durch Betrachtung des Grenzübergangs $h\rightarrow 0$ und $t\rightarrow \infty$. Für $t\rightarrow \infty$ strebt dieser Differenzenquotient gegen Null (Siehe hierzu Papadopoulos/Heavey/Browne 1993, S. 55f.). Damit entsteht folgendes Gleichungssystem für die stationären Zustandswahrscheinlichkeiten, $P_{n}, (n= 0,1,2)$:
$-\lambda \cdot P_{0} + \mu \cdot P_{1} =0$
$\lambda \cdot P_{0}-(\lambda +\mu )\cdot P_{1}+\mu \cdot P_{2}=0$
$\lambda \cdot P_{1}-\mu \cdot P_{2}=0 $
oder
$\lambda \cdot P_{0}=\mu \cdot P_{1}\qquad $(a)
$(\lambda +\mu )\cdot P_{1}=\lambda \cdot P_{0}+\mu \cdot P_{2}\qquad$ (b)
$\mu \cdot P_{2}=\lambda \cdot P_{1}\qquad$ (c)
Aus (a) folgt
$P_{1}=\frac{\lambda}{ \mu }\cdot P_{0}\qquad $(d)
Aus (b) folgt
$P_{2}=\frac{\lambda}{ \mu }\cdot P_{1}+P_{1}-\frac{\lambda}{ \mu }\cdot P_{0}$
$P_{2}=\left( {\frac{\lambda }{ \mu }} \right)^2\cdot P_{0}+\frac{\lambda }{ \mu }\cdot P_{0}-\frac{\lambda }{ \mu }\cdot P_{0}$
$P_{2}=\left( {\frac{\lambda }{ \mu }} \right)^2\cdot P_{0} \qquad $(e)
Berücksichtigen wir nun, daß die Summe aller Wahrscheinlichkeiten 1 betragen muß:
$P_{0}+P_{1}+P_{2}=1 \qquad $(f)
Wir erhalten dann durch einsetzen von (d) und (e) in (f)
$P_{0}+\frac{\lambda}{ \mu }\cdot P_{0}+\left( {\frac{\lambda }{ \mu }} \right)^2\cdot P_{0}=1$
Daraus folgt
$P_{0}=\frac{1}{1+\frac{\lambda }{ \mu }+\left( {\frac{\lambda}{ \mu }} \right)^2}\qquad$(g)
Im Nenner von (g) steht eine geometrische Reihe, deren Elemente sich durch einen konstanten Faktor $\frac{\lambda}{\mu}$ unterscheiden: $({\frac{\lambda}{\mu}})^0, ({\frac{\lambda}{\mu}})^1, ({\frac{\lambda}{\mu}})^2$. Die Summe einer geometischen Reihe mit $n+1$ Gliedern, $s_n=a_0+a_1+...+a_n=a\cdot (1+q^1+q^2+...+q^n)$ beträgt $s_n=a\cdot \frac {1-q^{n+1}}{1-q}$.
Im vorliegenden Fall ergibt sich wegen $n=2$ und $a=1$:
$P_{0}=\frac{1}{\frac{ 1-\left( {\frac{\lambda }{ \mu }} \right)^3}{ 1-\frac{\lambda }{ \mu}$
oder
$P_{0}=\frac { 1-\frac{\lambda}{ \mu }}{1-\left( {\frac{\lambda }{ \mu }} \right)^3}$
Allgemein gilt bei $N+1=c+3$ Zuständen:
$\lambda \cdot P_{0}=\mu \cdot P_{1}\quad$
$(\lambda +\mu )\cdot P_{n}=\lambda \cdot P_{n-1}+\mu \cdot P_{n+1}\quad 1\leq n\leq N\quad$
$\mu \cdot P_{N}=\lambda \cdot P_{N-1}\quad$
Für $P_0$ ergibt sich dann
$P_0=\frac{1-(\frac{\lambda}{\mu})}{1-(\frac{\lambda}{\mu})^{N+1}}$
oder
$P_0=\frac{1-\rho}{1-\rho^{N+1}}$
Dieses Ergebnis ist identisch mit $P_0$ für ein $(M/M/1):(GD/N/\infty)$-Warteschlangensystem, wenn man die Produktionsrate der ersten Station als Ankunftsrate $\lambda$ und die Produktionsrate der zweiten Station als Bedienrate $\mu$ interpretiert. Das sieht dann so aus:
Die gesuchte Produktionsrate kann mit Hilfe von $P_0$ wie folgt ermittelt werden:
$X=(1-P_0) \cdot \mu$
Mehr ...
Literatur
| Günther, H.-O. und H. Tempelmeier (2012). Produktion und Logistik (9. Aufl.). Berlin: Springer. |
| Tempelmeier, H. (2010), Supply Chain Management und Produktion - Übungen und Mini-Fallstudien. 3. Aufl., Norderstedt: Books on Demand. |